湿り空気 水分を含んでいる空気のことを「湿り空気」と呼びます。
これに対して、まったく水分を含まない空気を「乾き空気」といいます。
空気線図
空気線図(Psychrometric Chart)」とは、湿り空気がいろいろな状態にあるときのポイント
状態点)を、
二次元座標にプロットしてチャートにしたものです。
いろいろな種類がありますが、ごく一般に空気線図というとき、
それは、「湿り空気h-x線図」を示します。
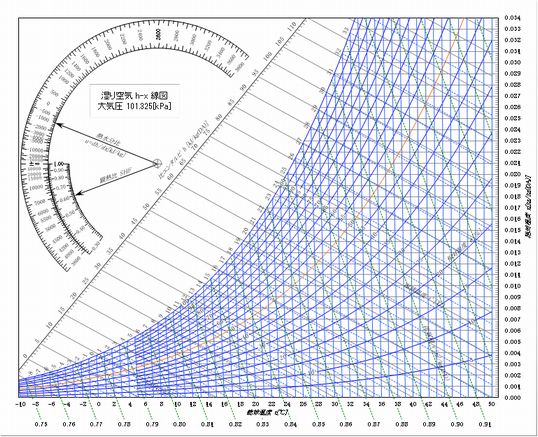
上の画像は、エクセル空気線図G2が使用しているh-x線図です。
なぜh-x線図というかといえば、hとxを座標軸としているからです。
(画像にマウスカーソルをのせてみてください)
hとは比エンタルピ[kJ/kg(DA)]で、空気の持っている熱量を示し、
xとは絶対湿度[kg/kg(DA)]で乾き空気1[kg]に含まれている水分の重さ[kg]を示します。
単位の末尾に(DA)と書いているのは乾き空気(Dry Air)を基準にしていることを意味します。
左上から右下に向かって実線で描かれている線はh一定の線、
水平に引かれている線がx一定の線です。
奇妙なことに、座標軸が斜めに交わっているのですね。このような座標のことを斜交座標といいます。
ではなぜ斜交座標なのでしょう。
二次元座標にプロットしてチャートにしたものです。
いろいろな種類がありますが、ごく一般に空気線図というとき、
それは、「湿り空気h-x線図」を示します。

上の画像は、エクセル空気線図G2が使用しているh-x線図です。
なぜh-x線図というかといえば、hとxを座標軸としているからです。
(画像にマウスカーソルをのせてみてください)
hとは比エンタルピ[kJ/kg(DA)]で、空気の持っている熱量を示し、
xとは絶対湿度[kg/kg(DA)]で乾き空気1[kg]に含まれている水分の重さ[kg]を示します。
単位の末尾に(DA)と書いているのは乾き空気(Dry Air)を基準にしていることを意味します。
左上から右下に向かって実線で描かれている線はh一定の線、
水平に引かれている線がx一定の線です。
奇妙なことに、座標軸が斜めに交わっているのですね。このような座標のことを斜交座標といいます。
ではなぜ斜交座標なのでしょう。
乾球温度と湿球温度
ふつう私たちが「気温」というとき、それは乾球温度[℃]を示します。
乾球温度は普通の温度計で測った空気の温度です。
皆様は小学生のころ、「百葉箱」の中をのぞいたことがありますか?
「百葉箱」の中には、普通の温度計のほかに、
温度計のお尻に濡れたガーゼを巻きつけてあるものがありませんでしたか?
あれは何を測っているかといえば、湿球温度[℃]なんです。
温度計の湿ったお尻(球)の温度です。
湿球温度というのは、水が自然に蒸発していくときにそれに触れている温度計が示す温度です。
もちろん、ちゃんと測るときはもっと精巧にできた測定器を使用しますが・・・
乾球温度は普通の温度計で測った空気の温度です。
皆様は小学生のころ、「百葉箱」の中をのぞいたことがありますか?
「百葉箱」の中には、普通の温度計のほかに、
温度計のお尻に濡れたガーゼを巻きつけてあるものがありませんでしたか?
あれは何を測っているかといえば、湿球温度[℃]なんです。
温度計の湿ったお尻(球)の温度です。
湿球温度というのは、水が自然に蒸発していくときにそれに触れている温度計が示す温度です。
もちろん、ちゃんと測るときはもっと精巧にできた測定器を使用しますが・・・
比エンタルピ
完全な乾き空気は、普通私たちのまわりにはありませんが、
空気のことを調べていくときにはまずここからスタートしないと良くわかりません。
実は比エンタルピの「比」というのは、「何かに比べた」という意味なんです。
その「何か」とは0[℃]の乾き空気が持っている熱量です。
比エンタルピの定義は以下のとおり。
h=Cpa・t+(Cpw・t+r0)・x ・・・(1)
h:比エンタルピ[kJ/kg(DA)]、
Cpa:乾き空気の定圧比熱[kJ/kg・K]、Cpw:水蒸気の定圧比熱[kJ/kg・K]、
t:乾球温度[℃]、r0:0[℃]のときの水の蒸発熱[kJ/kg]、x:絶対湿度[kg/kg(DA)]
空気のことを調べていくときにはまずここからスタートしないと良くわかりません。
実は比エンタルピの「比」というのは、「何かに比べた」という意味なんです。
その「何か」とは0[℃]の乾き空気が持っている熱量です。
比エンタルピの定義は以下のとおり。
h=Cpa・t+(Cpw・t+r0)・x ・・・(1)
h:比エンタルピ[kJ/kg(DA)]、
Cpa:乾き空気の定圧比熱[kJ/kg・K]、Cpw:水蒸気の定圧比熱[kJ/kg・K]、
t:乾球温度[℃]、r0:0[℃]のときの水の蒸発熱[kJ/kg]、x:絶対湿度[kg/kg(DA)]
水のこと
ここで、少しだけ水について考えましょう。
水は私たちの生活空間の中で、3つの姿を見せてくれますね。
もちろん最初は「水」、そしてうんと冷やしていくと「氷」になり、
ほおっておけば蒸発して「水蒸気」になります。
水は0.01[℃]のとき、この3つの姿をそれぞれ同時に持つことができます。
この温度0.01[℃]の状態を示す点のことを「水の三重点」と呼びます。
0[℃]よりちょっとだけずれているんです。
水は私たちの生活空間の中で、3つの姿を見せてくれますね。
もちろん最初は「水」、そしてうんと冷やしていくと「氷」になり、
ほおっておけば蒸発して「水蒸気」になります。
水は0.01[℃]のとき、この3つの姿をそれぞれ同時に持つことができます。
この温度0.01[℃]の状態を示す点のことを「水の三重点」と呼びます。
0[℃]よりちょっとだけずれているんです。
飽和水蒸気圧
乾き空気にどんどん、どんどん、水を蒸発させていくと、あるところで限界になります。
つまり、それ以上水を含むことができなくなるのです。
このときの、水蒸気の圧力は、温度によって一定です。この圧力を「飽和水蒸気圧」といいます。
実は湿り空気はとても複雑な性質を持っていて、その状態を簡単に計算することができません。
それでも何か確たるものがなければ先に進まないのですが、
この飽和水蒸気圧が温度によって一意的に決まるという性質こそが、
湿り空気を解き明かしていく上での最初の手がかりになってくれます。
つまり、それ以上水を含むことができなくなるのです。
このときの、水蒸気の圧力は、温度によって一定です。この圧力を「飽和水蒸気圧」といいます。
実は湿り空気はとても複雑な性質を持っていて、その状態を簡単に計算することができません。
それでも何か確たるものがなければ先に進まないのですが、
この飽和水蒸気圧が温度によって一意的に決まるという性質こそが、
湿り空気を解き明かしていく上での最初の手がかりになってくれます。
Wexler-Hylandの式
飽和水蒸気圧が温度によって決まるのなら、そこには当然関係式があるはずです。
Sonntagの式、Goff-Gratchの式など様々なものがありますが、
空気調和・衛生工学会が採用しており、現在最も一般的と言えるのが、
「Wexler-Hylandの式」
と呼ばれるものです。
いくつかのサイトで紹介されているようですが、
もう一度Wexler-Hylandの式を確認しましょう。
水と接するとき(0.01[℃]以上)
ln(103Ps)
=-0.58002206×104/Tab
+0.13914993×10
-0.48640239×10-1Tab
+0.41764768×10-4Tab2
-0.14452093×10-7Tab3
+0.65459673×10 ln(Tab) ・・・・(2.1)
氷と接するとき(0.01[℃]以下)
ln(103Ps)
=-0.56745359×104/Tab
+0.63925247×10
-0.96778430×10-2Tab
+0.62215701×10-6Tab2
+0.20747825×10-8Tab3
-0.94840240×10-12Tab4
+0.41635019×10 ln(Tab) ・・・(2.2)
ここにPs:飽和水蒸気圧[kPa]、Tab=絶対温度[K](=セルシウス温度+273.15)
上の式をPsについて解くと、 Ps=[exp{-0.58002206×104/Tab+・・・・・}]×10-3
という形になりますが、それよりもエクセル湿り空気G2をお使いください。
飽和水蒸気圧の計算関数をはじめ、エクセル湿り空気G2は多くの関数をフリーソフトとして公開しています。
また、エクセル空気線図G2にはエクセル湿り空気G2が標準添付されています。
さらにエクセル空気線図G2では、
上記Psに、温度と圧力による補正係数fsを乗じ、より現実の湿り空気に近い状態値を計算しています。
Sonntagの式、Goff-Gratchの式など様々なものがありますが、
空気調和・衛生工学会が採用しており、現在最も一般的と言えるのが、
「Wexler-Hylandの式」
と呼ばれるものです。
いくつかのサイトで紹介されているようですが、
もう一度Wexler-Hylandの式を確認しましょう。
水と接するとき(0.01[℃]以上)
ln(103Ps)
=-0.58002206×104/Tab
+0.13914993×10
-0.48640239×10-1Tab
+0.41764768×10-4Tab2
-0.14452093×10-7Tab3
+0.65459673×10 ln(Tab) ・・・・(2.1)
氷と接するとき(0.01[℃]以下)
ln(103Ps)
=-0.56745359×104/Tab
+0.63925247×10
-0.96778430×10-2Tab
+0.62215701×10-6Tab2
+0.20747825×10-8Tab3
-0.94840240×10-12Tab4
+0.41635019×10 ln(Tab) ・・・(2.2)
ここにPs:飽和水蒸気圧[kPa]、Tab=絶対温度[K](=セルシウス温度+273.15)
上の式をPsについて解くと、 Ps=[exp{-0.58002206×104/Tab+・・・・・}]×10-3
という形になりますが、それよりもエクセル湿り空気G2をお使いください。
飽和水蒸気圧の計算関数をはじめ、エクセル湿り空気G2は多くの関数をフリーソフトとして公開しています。
また、エクセル空気線図G2にはエクセル湿り空気G2が標準添付されています。
さらにエクセル空気線図G2では、
上記Psに、温度と圧力による補正係数fsを乗じ、より現実の湿り空気に近い状態値を計算しています。
相対湿度
「飽和水蒸気圧」なんて言葉は知らなくても「相対湿度」ならご存知でしょうか。
実はこの「相対湿度」とは、水蒸気分圧/飽和水蒸気圧 ×100[%]なのです。
ここで水蒸気分圧というのは、読んで字のごとく水蒸気の分の圧力です。
つまり、水蒸気分圧=飽和水蒸気圧のときが相対湿度=100[%]で、
この状態の空気のことを「飽和空気」といいます。
また、湿り空気が「飽和空気」の状態にあるとき、乾球温度=湿球温度になります。
これはちょっと考えればわかることで、飽和してるときは、水がもうこれ以上蒸発しないのですから、
温度計のお尻が濡れていようがいまいが、同じことになるからですね。
実はこの「相対湿度」とは、水蒸気分圧/飽和水蒸気圧 ×100[%]なのです。
ここで水蒸気分圧というのは、読んで字のごとく水蒸気の分の圧力です。
つまり、水蒸気分圧=飽和水蒸気圧のときが相対湿度=100[%]で、
この状態の空気のことを「飽和空気」といいます。
また、湿り空気が「飽和空気」の状態にあるとき、乾球温度=湿球温度になります。
これはちょっと考えればわかることで、飽和してるときは、水がもうこれ以上蒸発しないのですから、
温度計のお尻が濡れていようがいまいが、同じことになるからですね。
絶対湿度
実際にはもっともっと複雑なのですが、ここである程度の精度を持った式をご紹介します。
x=0.62198×Pw/(P-Pw) ・・・(3)
x:絶対湿度[kg/kg(DA)]、Pw:水蒸気分圧[kPa]、P:空気の全圧[kPa]
ここでPは、普通は海抜0mの大気圧(101.325[kPa])で計算します。
x=0.62198×Pw/(P-Pw) ・・・(3)
x:絶対湿度[kg/kg(DA)]、Pw:水蒸気分圧[kPa]、P:空気の全圧[kPa]
ここでPは、普通は海抜0mの大気圧(101.325[kPa])で計算します。
h-x線図とt-x線図
さあ、ここでようやく空気線図の話に戻ります。
h-x線図がなぜ斜交座標なのか・・・でしたね。
(1)、(2)、(3)式をご覧いただくとお分かりと思いますが、(代数的な細かい話は省略します)
乾球温度 t [℃] を座標軸にして t の線を平行に引くと、比エンタルピの線が平行でなくなります。
このような空気線図を「t-x線図」といいます。簡略化した空気線図のほとんどはこの「t-x線図」です。
空気線図の大きな使用目的のひとつである「熱量の変化を求める」という観点からすると、
熱量すなわち比エンタルピを示す線が平行でないのは非常に具合が悪いのです。
でも直感しやすいのは乾球温度。
それでこのような特殊な座標系になったのではないかと思われます。
「t-x線図」においては熱水分比またはSHFのラインは、その傾きが起点により変化します。
したがって、エクセル空気線図G2が出力する空気線図のような、熱水分比やSHFを示す円弧は描けません。
h-x線図がなぜ斜交座標なのか・・・でしたね。
(1)、(2)、(3)式をご覧いただくとお分かりと思いますが、(代数的な細かい話は省略します)
乾球温度 t [℃] を座標軸にして t の線を平行に引くと、比エンタルピの線が平行でなくなります。
このような空気線図を「t-x線図」といいます。簡略化した空気線図のほとんどはこの「t-x線図」です。
空気線図の大きな使用目的のひとつである「熱量の変化を求める」という観点からすると、
熱量すなわち比エンタルピを示す線が平行でないのは非常に具合が悪いのです。
でも直感しやすいのは乾球温度。
それでこのような特殊な座標系になったのではないかと思われます。
「t-x線図」においては熱水分比またはSHFのラインは、その傾きが起点により変化します。
したがって、エクセル空気線図G2が出力する空気線図のような、熱水分比やSHFを示す円弧は描けません。
h-x線図における乾球温度ラインの傾き
少々目が痛いかもしれませんが、
もう一度この「空気線図」セクションの冒頭にある空気線図を目を凝らしてじっくり眺めてください。
(画像をクリックするとわかりやすいかもしれません)
なになに、乾球温度一定の線が傾いている・・・コリャ印刷ミス、ならぬ描画ミス?
実はh-x線図はどうしてもこうなってしまうのです。
代数的な細かい話は省略しますが、結論だけ申し上げれば、
絶対湿度の値が大きくなると、直交座標上の乾球温度の目盛りは広がっていくのです。
h-x線図は普通、これは紙面の節約という意味からでしょうが、
右端の乾球温度一定の線がx一定の線に直交するように描かれます。
その結果、乾球温度が低くなればなるほど、
乾球温度一定の線は、ピサの斜塔のごとく左に傾くことになります。
もう一度この「空気線図」セクションの冒頭にある空気線図を目を凝らしてじっくり眺めてください。
(画像をクリックするとわかりやすいかもしれません)
なになに、乾球温度一定の線が傾いている・・・コリャ印刷ミス、ならぬ描画ミス?
実はh-x線図はどうしてもこうなってしまうのです。
代数的な細かい話は省略しますが、結論だけ申し上げれば、
絶対湿度の値が大きくなると、直交座標上の乾球温度の目盛りは広がっていくのです。
h-x線図は普通、これは紙面の節約という意味からでしょうが、
右端の乾球温度一定の線がx一定の線に直交するように描かれます。
その結果、乾球温度が低くなればなるほど、
乾球温度一定の線は、ピサの斜塔のごとく左に傾くことになります。
h-x線図のおさらい
冒頭にある空気線図の水平に引かれているのは絶対湿度、
左上から右下に引かれているのが比エンタルピ、
縦に伸びているのが乾球温度、そして美しい曲線を描いているのは相対湿度のラインです。
これが空気線図の基本ですが、
そのほかに、湿球温度、比容積、飽和度など必要に応じてそのラインが描かれます。
左上から右下に引かれているのが比エンタルピ、
縦に伸びているのが乾球温度、そして美しい曲線を描いているのは相対湿度のラインです。
これが空気線図の基本ですが、
そのほかに、湿球温度、比容積、飽和度など必要に応じてそのラインが描かれます。
h-x線図上における変化のプロセスまたは状態線
h-x線図上で空気がある勾配をもって変化するときの様子を示したものを「状態線」といいますが、
いくつかの状態線もしくは状態変化のプロセスについて簡単にご説明しましょう。
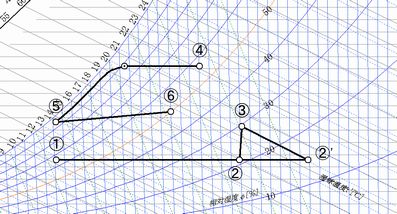
上の画像はエクセル湿り空気G2の状態関数を用いて状態点または状態線をプロットし、
必要部分を切り取ったものです。
この画像をご覧頂きながら、代表的なパターンについてご説明しましょう。
【水分量(絶対湿度)の変化を伴わない温度変化 ①→②(②')】
このような変化のことを、「顕熱変化」といいますが、たとえばある状態の空気を単純にヒーターで暖めると
その状態点は、絶対湿度一定で乾球温度だけが上がりますので、そのプロセスを示す線は水平になります。
さて、冬場、風邪をひきやすい方、加湿器がないなら、暖房を少し控えめにしてみてください。
たとえば東京では、真冬の外気が0[℃]、50[%]程度になることがありますが、
(冒頭の空気線図で0[℃]、50[%]の状態点がどこであるかお分かりでしょうか?)
この状態から26[℃]まで温度を上げると、相対湿度は約9[%]まで下がります。
もし、18[℃]で我慢すれば、相対湿度は約15[%]。
相対湿度の値が大きいと、水分が蒸発しにくくなりますので、のどがからからになりにくくなります。
とかく風邪をひきやすいと、暖房をめいっぱいきかせたくなりますが、
これはある意味では逆効果になってしまいます。
【水分量(絶対湿度)の変化を伴う温度変化 ④→⑤】
ある状態の空気を冷やしていくと、やがて相対湿度が100[%]のラインに交わります。
これは飽和空気の状態を示し、それ以上まっすぐ左には行けなくなります。
このときの温度を「露点温度」といいますが、
実際に冷却装置で冷却するときは、相対湿度が95[%]程度のところで限界になり、
今度は相対湿度一定のラインにそって左下に下りていきます。
このとき冷却装置の内部では水蒸気がどんどん水になって滴り落ちていきます。
水蒸気が水になれば、空気中の水分量は減少しますので空気は乾燥していきます。
そこでこのような動きを受動的に「減湿」、能動的に「除湿」等といいます。
ここで単純に水平方向に変化する場合と、
減湿を伴う変化の場合の比エンタルピの変化量に注目してください。
そうです。減湿を伴う変化が起きると、エンタルピ、すなわち空気の熱量は大きく変化するのです。
これは、同じ温度の変化なら、たいてい暖房よりも冷房のときのほうがエンタルピの変化が大きい、
つまりエネルギーの変化量が大きいということです。
別の言い方をすれば、冷房をするときの消費エネルギーは非常に大きいのです。
特に夏暑い日、外気(冷房していない外の空気)が多く入りこんでくる場合、
冷房をするときの温度を1[℃]上げるだけで、
それにかかわるエネルギーの消費量が大幅に減るわけです。
青く美しい地球を大切にするためにも、冷房の温度には気をつけたいですね。
なお、「結露」という言葉がありますが、
これは湿り空気がその露点温度よりも低いものに接し、
(あるいは自然に温度が下がって露点温度以下になり)
水蒸気が凝縮して水になるために起こる現象で、
そのプロセスは、上記の「減湿」と同じものです。
暑い夏の日、ビールやアイスコーヒーを注いだグラスの表面にうっすらとついた白い水滴が涼しそうですね。
これも、グラスの表面で湿り空気が冷却されて結露した結果です。
【水で加湿をするときの変化 ②'→③】
ここから先はかなり専門的ですので、結論だけ申し上げます。
まずは、h-x線図上ではある熱水分比(比エンタルピの変化量/絶対湿度の変化量)による状態線は、
その起点によらず一定の傾きをもっているということを知っておいてください。
(これも代数的に明らかにすることができますが、ここでは省略します。)
水で加湿をするときの変化を示す状態線は、湿球温度一定の線上にあります。
別の言い方をすると、湿球温度が与える熱水分比によって決められる熱水分比一定の状態線になります。
このときの熱水分比は以下のとおり
水と接するとき、つまり温度計のお尻のガーゼが凍っていないとき(0.01[℃]以上)
u=Cw・t'
氷と接するとき(0.01[℃]以下)
u=-rc+Cc・t'
ここに
t':湿球温度[℃]
u:水加湿をするときのt'により決まる熱水分比[kJ/kg]
Cw:水の比熱[kJ/kg・K]、Cc:氷の比熱[kJ/kg・K]、rc:氷の融解熱[kJ/kg]
【蒸気で加湿をするときの変化 ②→③】
加湿する蒸気の比エンタルピを熱水分比とする熱水分比一定の状態線になります。
水で加湿をすると(たとえば家庭用の超音波加湿器など)、温度は下がります。
ところが蒸気で加湿をすると、普通、少しだけ温度が上がります。
昔の人は、火の上にやかんを置いて加湿していましたが、とても良い加湿方法を用いていたのですね。
(安全上、火の上にやかんなどを置くことはお勧めできませんが)
【冷房時の室内の温湿度変化 ⑤→⑥】
SHF(顕熱比=Sensible Heat Factor)と呼ばれる比率が与える熱水分比によって決められる、
熱水分比一定の状態線になります。
ちなみに、SHFの定義は以下のとおり。
SHF=顕熱/(顕熱+潜熱)
さらにSHFとほかのファクターの関係は
SHF=Cpa・⊿t/⊿h=1-(r0+Cpw・⊿t)/u
顕熱:乾き空気の温度変化による熱量
潜熱:水の蒸発および温度変化による熱量
⊿t:温度の変化量[K]、⊿h:比エンタルピの変化量[kJ/kg(DA)]、u:SHFがある値のときの熱水分比[kJ/kg]
いくつかの状態線もしくは状態変化のプロセスについて簡単にご説明しましょう。

上の画像はエクセル湿り空気G2の状態関数を用いて状態点または状態線をプロットし、
必要部分を切り取ったものです。
この画像をご覧頂きながら、代表的なパターンについてご説明しましょう。
【水分量(絶対湿度)の変化を伴わない温度変化 ①→②(②')】
このような変化のことを、「顕熱変化」といいますが、たとえばある状態の空気を単純にヒーターで暖めると
その状態点は、絶対湿度一定で乾球温度だけが上がりますので、そのプロセスを示す線は水平になります。
さて、冬場、風邪をひきやすい方、加湿器がないなら、暖房を少し控えめにしてみてください。
たとえば東京では、真冬の外気が0[℃]、50[%]程度になることがありますが、
(冒頭の空気線図で0[℃]、50[%]の状態点がどこであるかお分かりでしょうか?)
この状態から26[℃]まで温度を上げると、相対湿度は約9[%]まで下がります。
もし、18[℃]で我慢すれば、相対湿度は約15[%]。
相対湿度の値が大きいと、水分が蒸発しにくくなりますので、のどがからからになりにくくなります。
とかく風邪をひきやすいと、暖房をめいっぱいきかせたくなりますが、
これはある意味では逆効果になってしまいます。
【水分量(絶対湿度)の変化を伴う温度変化 ④→⑤】
ある状態の空気を冷やしていくと、やがて相対湿度が100[%]のラインに交わります。
これは飽和空気の状態を示し、それ以上まっすぐ左には行けなくなります。
このときの温度を「露点温度」といいますが、
実際に冷却装置で冷却するときは、相対湿度が95[%]程度のところで限界になり、
今度は相対湿度一定のラインにそって左下に下りていきます。
このとき冷却装置の内部では水蒸気がどんどん水になって滴り落ちていきます。
水蒸気が水になれば、空気中の水分量は減少しますので空気は乾燥していきます。
そこでこのような動きを受動的に「減湿」、能動的に「除湿」等といいます。
ここで単純に水平方向に変化する場合と、
減湿を伴う変化の場合の比エンタルピの変化量に注目してください。
そうです。減湿を伴う変化が起きると、エンタルピ、すなわち空気の熱量は大きく変化するのです。
これは、同じ温度の変化なら、たいてい暖房よりも冷房のときのほうがエンタルピの変化が大きい、
つまりエネルギーの変化量が大きいということです。
別の言い方をすれば、冷房をするときの消費エネルギーは非常に大きいのです。
特に夏暑い日、外気(冷房していない外の空気)が多く入りこんでくる場合、
冷房をするときの温度を1[℃]上げるだけで、
それにかかわるエネルギーの消費量が大幅に減るわけです。
青く美しい地球を大切にするためにも、冷房の温度には気をつけたいですね。
なお、「結露」という言葉がありますが、
これは湿り空気がその露点温度よりも低いものに接し、
(あるいは自然に温度が下がって露点温度以下になり)
水蒸気が凝縮して水になるために起こる現象で、
そのプロセスは、上記の「減湿」と同じものです。
暑い夏の日、ビールやアイスコーヒーを注いだグラスの表面にうっすらとついた白い水滴が涼しそうですね。
これも、グラスの表面で湿り空気が冷却されて結露した結果です。
【水で加湿をするときの変化 ②'→③】
ここから先はかなり専門的ですので、結論だけ申し上げます。
まずは、h-x線図上ではある熱水分比(比エンタルピの変化量/絶対湿度の変化量)による状態線は、
その起点によらず一定の傾きをもっているということを知っておいてください。
(これも代数的に明らかにすることができますが、ここでは省略します。)
水で加湿をするときの変化を示す状態線は、湿球温度一定の線上にあります。
別の言い方をすると、湿球温度が与える熱水分比によって決められる熱水分比一定の状態線になります。
このときの熱水分比は以下のとおり
水と接するとき、つまり温度計のお尻のガーゼが凍っていないとき(0.01[℃]以上)
u=Cw・t'
氷と接するとき(0.01[℃]以下)
u=-rc+Cc・t'
ここに
t':湿球温度[℃]
u:水加湿をするときのt'により決まる熱水分比[kJ/kg]
Cw:水の比熱[kJ/kg・K]、Cc:氷の比熱[kJ/kg・K]、rc:氷の融解熱[kJ/kg]
【蒸気で加湿をするときの変化 ②→③】
加湿する蒸気の比エンタルピを熱水分比とする熱水分比一定の状態線になります。
水で加湿をすると(たとえば家庭用の超音波加湿器など)、温度は下がります。
ところが蒸気で加湿をすると、普通、少しだけ温度が上がります。
昔の人は、火の上にやかんを置いて加湿していましたが、とても良い加湿方法を用いていたのですね。
(安全上、火の上にやかんなどを置くことはお勧めできませんが)
【冷房時の室内の温湿度変化 ⑤→⑥】
SHF(顕熱比=Sensible Heat Factor)と呼ばれる比率が与える熱水分比によって決められる、
熱水分比一定の状態線になります。
ちなみに、SHFの定義は以下のとおり。
SHF=顕熱/(顕熱+潜熱)
さらにSHFとほかのファクターの関係は
SHF=Cpa・⊿t/⊿h=1-(r0+Cpw・⊿t)/u
顕熱:乾き空気の温度変化による熱量
潜熱:水の蒸発および温度変化による熱量
⊿t:温度の変化量[K]、⊿h:比エンタルピの変化量[kJ/kg(DA)]、u:SHFがある値のときの熱水分比[kJ/kg]
状態点の計算
h-x線図は二次元座標に描かれたチャートです。
理論的には、ある2要素が決まればその状態点は決まります。
しかしながら、湿り空気はそう単純なものではなく、
仮にそれがボイル-シャルルの法則に従う、
理想気体としての乾き空気と水蒸気の混合気体であったとしても、
そのすべての関係式が代数的に与えられているわけではありません。
どうしても近似計算が必要になります。
そこで登場するのがコンピューターです。
コンピューターで効率よく近似計算をする手法には、
1.二分法
2.ニュートン - ラフソン法
などがあります。コンピュータを用いた近似計算に関しては、
詳しく解説されているサイトがいくつもありますので省略します。
コンピューターが十分高速化している今、湿り空気の状態点の計算には、二分法が適しています。
理論的には、ある2要素が決まればその状態点は決まります。
しかしながら、湿り空気はそう単純なものではなく、
仮にそれがボイル-シャルルの法則に従う、
理想気体としての乾き空気と水蒸気の混合気体であったとしても、
そのすべての関係式が代数的に与えられているわけではありません。
どうしても近似計算が必要になります。
そこで登場するのがコンピューターです。
コンピューターで効率よく近似計算をする手法には、
1.二分法
2.ニュートン - ラフソン法
などがあります。コンピュータを用いた近似計算に関しては、
詳しく解説されているサイトがいくつもありますので省略します。
コンピューターが十分高速化している今、湿り空気の状態点の計算には、二分法が適しています。
自然界にあるものはやはり美しい
湿り空気h-x線図は、私たちを取り巻いている「潤いある空気」を視覚的にあらわしたものですが、
結果的に、そこに描かれた相対湿度のラインはなんとも美しく、
ここでもまた、自然界に存在するものの美しさを再確認できるのではないでしょうか。
結果的に、そこに描かれた相対湿度のラインはなんとも美しく、
ここでもまた、自然界に存在するものの美しさを再確認できるのではないでしょうか。
代表的な3つの空気線図
今度は少し実践的なことを考えてみましょう。
まず、一般的に用いられている3種類の空気線図をご覧ください。
と言っても、すべては同じ「湿り空気 h-x 線図」なのですが表示している乾球温度、絶対湿度のレンジが異なるだけです。
最も一般的なのが、-10[℃]~50[℃]までの範囲を示したもので、NC線図などと呼ばれることもあります。
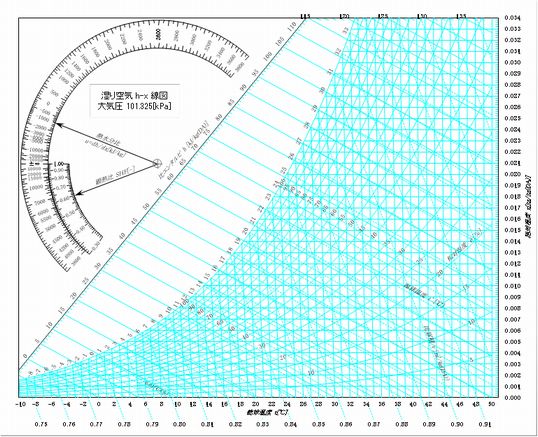
寒冷地でない限り、ほとんどの地域における一般的な環境下の状態点はこの空気線図で示すことができます。
次は主に冷凍庫などで使用するためのもので-50[℃]~10[℃]までの範囲を示したものです。
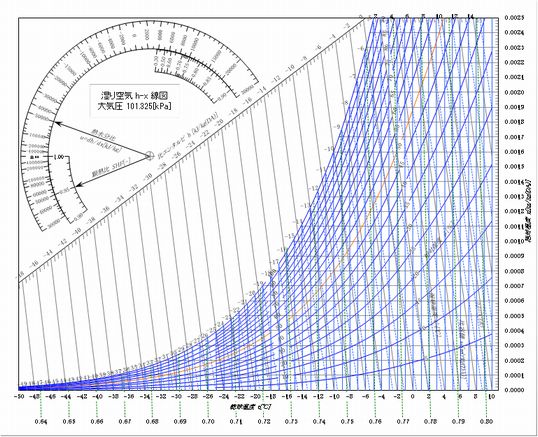
最初の空気線図を0[℃]を挟んでちょうど対象にした形で、LC線図などと呼ばれることもあります。
3つ目の空気線図は高温域です。
「空気調和・衛生工学便覧」(Ref1)では、
0[℃]~200[℃]、絶対湿度は0[kg/kg(DA)]~0.2[kg/kg(DA)]までの範囲のものが掲載されていますが、
エクセル空気線図G2では、実用性を重視して-10[℃]~190[℃]、
絶対湿度は大気圧101.325[kPa]下で0[kg/kg(DA)]~0.034[kg/kg(DA)]までとしています。
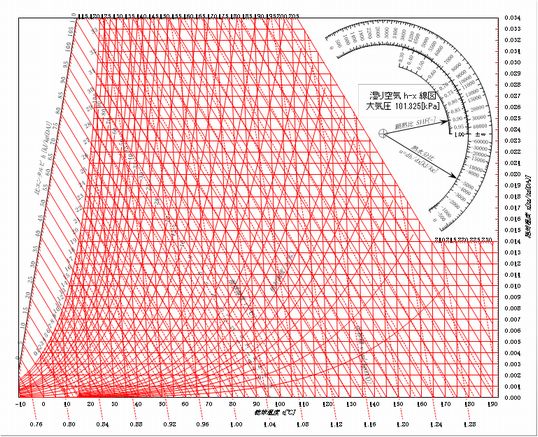
高温域の用途はやや特殊ですが、例えば高温再生形のデシカントシステムや、流動層造粒乾燥機用の空調機などでしょうか。
HC線図などと呼ばれることもあります。
ちょっと横道にそれますが、この空気線図の熱水分比スケール(右上の大きい方の円弧)をご覧ください。
左上の熱水分比0の目盛りと右下の0の目盛りを結んだ線が比エンタルピラインに平行ですね。
そうです。熱水分比=0とは、比エンタルピの変化がないということです。(比エンタルピの話は後ほど)
まず、一般的に用いられている3種類の空気線図をご覧ください。
と言っても、すべては同じ「湿り空気 h-x 線図」なのですが表示している乾球温度、絶対湿度のレンジが異なるだけです。
最も一般的なのが、-10[℃]~50[℃]までの範囲を示したもので、NC線図などと呼ばれることもあります。

寒冷地でない限り、ほとんどの地域における一般的な環境下の状態点はこの空気線図で示すことができます。
次は主に冷凍庫などで使用するためのもので-50[℃]~10[℃]までの範囲を示したものです。

最初の空気線図を0[℃]を挟んでちょうど対象にした形で、LC線図などと呼ばれることもあります。
3つ目の空気線図は高温域です。
「空気調和・衛生工学便覧」(Ref1)では、
0[℃]~200[℃]、絶対湿度は0[kg/kg(DA)]~0.2[kg/kg(DA)]までの範囲のものが掲載されていますが、
エクセル空気線図G2では、実用性を重視して-10[℃]~190[℃]、
絶対湿度は大気圧101.325[kPa]下で0[kg/kg(DA)]~0.034[kg/kg(DA)]までとしています。

高温域の用途はやや特殊ですが、例えば高温再生形のデシカントシステムや、流動層造粒乾燥機用の空調機などでしょうか。
HC線図などと呼ばれることもあります。
ちょっと横道にそれますが、この空気線図の熱水分比スケール(右上の大きい方の円弧)をご覧ください。
左上の熱水分比0の目盛りと右下の0の目盛りを結んだ線が比エンタルピラインに平行ですね。
そうです。熱水分比=0とは、比エンタルピの変化がないということです。(比エンタルピの話は後ほど)
標準形空調機の空気線図
次に標準形空調機の空気線図の作図方法を考えてみましょう。
ここでいう標準形空調機とは、外気と還気を混合し、冷却、加熱、加湿などを行うもので、これを示す空気線図は鉄板です。
下のようなフローです。
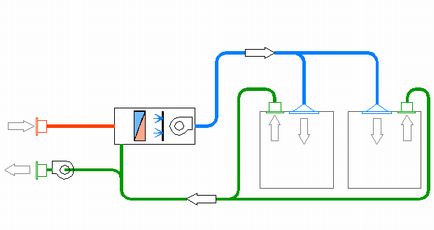
室内温湿度目標値は、冷房:28[℃],45[%]、暖房:19[℃],40[%]、
冷房顕熱負荷=17,565[W]、冷房潜熱負荷=1,848[W]、暖房(顕熱)負荷=7,671[W]、外気風量=840[m3/h]、
冷却コイル出口相対湿度=95[%]で、簡単のため、ファンやダクトによる温度上昇は無視します。
また、暖房時は浸透式(水)加湿器で加湿を行います。
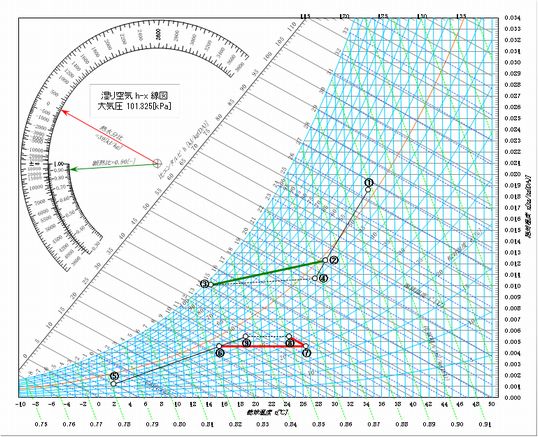
【手順1】冷房時の顕熱比SHFを計算します。すなわち顕熱比SHF=17,565/(17,565+1,848)≒0.90[-]。
【手順2】冷房時室内ポイント④をプロットし、④からSHF=0.90の状態線を引きます。
SHF=0.90の状態線(黒の破線部分)は、左上のSHFスケールを用いて引いたもの(緑色の線)と平行になるように引くのですが、
これがh-x線図が用いられる理由のひとつです。t-x線図ではこれができません。
この状態線と冷却コイル出口相対湿度(ここでは95[%])のラインの交点が、冷却コイル出口ポイント=冷房時吹出空気ポイント③です。
また、この状態線は冷房時の室内変化プロセスを示すことになります。
【手順3】冷房顕熱負荷から空調風量(空調に必要な風量)を計算します。
③の乾球温度は正確には14.96[℃]なので、冷房時の吹出温度差⊿tc=28-14.96=13.04[K]です。
空調風量=17,565/{(13.04/0.868)×1.006×(1,000/3,600)}≒4,190[m3/h] (一の位で切り上げ)
ここで0.868は冷房室内条件下における空気の比容積[m3/kg]注1なのですが、煩雑なら空気の密度の概算値1.2[kg/m3]を乗じてもかまいません。
1.006は乾き空気の定圧比熱[kJ/(kg・K)]です。
もしくは、乾き空気の容積比熱=乾き空気の定圧比熱/比容積=1.2[kJ/(m3・K)]として固定してしまう場合もあります。
【手順4】冷房時外気ポイント①をプロットします。
冷房時の外気は34.8[℃],52.6[%]とします。
【手順5】外気比を計算し、冷房時の外気-還気混合ポイント②をプロットします。
ポイント①の比容積=0.899[m3/kg]、ポイント④の比容積=0.868[m3/kg]として、
外気比=外気の質量/全給気空気(ここでは空調風量)の質量=(840/0.899)/[(840/0.899)+{(4,190-840)/0.868}]≒0.20[-]注2。
①と④を直線で結び、(②-④)/(①-④)=0.20となるポイントが混合ポイント②となります。
【手順6】②と③を直線で結びます。
このラインが冷却プロセスを示す状態線となります。
後ほど解説しますが、実際の冷却コイル内での変化は、最初は絶対湿度一定で、徐々に相対湿度95[%]のラインに接するように近づきます。
【手順7】暖房時の室内ポイント⑨をプロットします。
【手順8】暖房顕熱負荷と空調風量から、暖房時の吹出温度差⊿thを計算します。
⊿th=7,671/{(4,190/0.835)×1.006×(1,000/3,600)}≒5.47[K]
ここで0.835は暖房室内条件下における空気の比容積[m3/kg]注1なのですが、煩雑なら空気の密度の概算値1.2[kg/m3]を乗じてもかまいません。
1.006は乾き空気の定圧比熱[kJ/kg・K]です。
もしくは、乾き空気の容積比熱=乾き空気の定圧比熱/比容積=1.2[kJ/(m3・K)]として固定してしまう場合もあります。
【手順9】暖房時の吹出ポイント⑧をプロットします。
⑧は⑨から水平(絶対湿度一定)に温度のみを⊿th= 5.47[K]上げた状態点です
⑧と⑨を結びます。この状態線は暖房時の室内変化プロセスを示すことになります。
【手順10】暖房時の外気ポイント⑤をプロットします。
【手順11】暖房時の外気-還気混合ポイント⑥をプロットします。
冷房時と同様に外気比を計算し、外気比=0.19[-]注2、
⑤と⑨を直線で結び、(⑥-⑨)/(⑤-⑨)=0.19となるポイントが混合ポイント⑥となります。
【手順12】加熱コイル出口ポイント⑦をプロットします。
⑧から湿球温度ラインに平行な直線(湿球温度一定の状態線)を引き、
⑥から水平に引いた直線(絶対湿度一定の状態線)との交点が加熱コイル出口ポイント⑦です。
ここで⑥→⑦は加熱プロセス、⑦→⑧は水による加湿プロセスです。
注1:厳密には、比容積は吹出ポイントから室内ポイントまでの間に変化しますが、煩雑になりすぎるため、室内条件の時の値としています。
(特に、最小給気風量から逆算した値と比較しながらポイントを決定しなければならない場合などは収束計算が必要なため)
エクセル空気線図G2では低温域、高温域をサポートしているため、容積比熱としての固定値を使用せず、条件に応じた比容積を用いて計算しています。
注2:実務現場では計算プロセスが煩雑にならないよう、外気比は風量比としています。すなわち、
外気比=外気風量/全風量(ここでは空調風量)=840/4,190≒0.20[-]。
エクセル空気線図G2ではこちらの方法を用いています。
ここでいう標準形空調機とは、外気と還気を混合し、冷却、加熱、加湿などを行うもので、これを示す空気線図は鉄板です。
下のようなフローです。

室内温湿度目標値は、冷房:28[℃],45[%]、暖房:19[℃],40[%]、
冷房顕熱負荷=17,565[W]、冷房潜熱負荷=1,848[W]、暖房(顕熱)負荷=7,671[W]、外気風量=840[m3/h]、
冷却コイル出口相対湿度=95[%]で、簡単のため、ファンやダクトによる温度上昇は無視します。
また、暖房時は浸透式(水)加湿器で加湿を行います。

【手順1】冷房時の顕熱比SHFを計算します。すなわち顕熱比SHF=17,565/(17,565+1,848)≒0.90[-]。
【手順2】冷房時室内ポイント④をプロットし、④からSHF=0.90の状態線を引きます。
SHF=0.90の状態線(黒の破線部分)は、左上のSHFスケールを用いて引いたもの(緑色の線)と平行になるように引くのですが、
これがh-x線図が用いられる理由のひとつです。t-x線図ではこれができません。
この状態線と冷却コイル出口相対湿度(ここでは95[%])のラインの交点が、冷却コイル出口ポイント=冷房時吹出空気ポイント③です。
また、この状態線は冷房時の室内変化プロセスを示すことになります。
【手順3】冷房顕熱負荷から空調風量(空調に必要な風量)を計算します。
③の乾球温度は正確には14.96[℃]なので、冷房時の吹出温度差⊿tc=28-14.96=13.04[K]です。
空調風量=17,565/{(13.04/0.868)×1.006×(1,000/3,600)}≒4,190[m3/h] (一の位で切り上げ)
ここで0.868は冷房室内条件下における空気の比容積[m3/kg]注1なのですが、煩雑なら空気の密度の概算値1.2[kg/m3]を乗じてもかまいません。
1.006は乾き空気の定圧比熱[kJ/(kg・K)]です。
もしくは、乾き空気の容積比熱=乾き空気の定圧比熱/比容積=1.2[kJ/(m3・K)]として固定してしまう場合もあります。
【手順4】冷房時外気ポイント①をプロットします。
冷房時の外気は34.8[℃],52.6[%]とします。
【手順5】外気比を計算し、冷房時の外気-還気混合ポイント②をプロットします。
ポイント①の比容積=0.899[m3/kg]、ポイント④の比容積=0.868[m3/kg]として、
外気比=外気の質量/全給気空気(ここでは空調風量)の質量=(840/0.899)/[(840/0.899)+{(4,190-840)/0.868}]≒0.20[-]注2。
①と④を直線で結び、(②-④)/(①-④)=0.20となるポイントが混合ポイント②となります。
【手順6】②と③を直線で結びます。
このラインが冷却プロセスを示す状態線となります。
後ほど解説しますが、実際の冷却コイル内での変化は、最初は絶対湿度一定で、徐々に相対湿度95[%]のラインに接するように近づきます。
【手順7】暖房時の室内ポイント⑨をプロットします。
【手順8】暖房顕熱負荷と空調風量から、暖房時の吹出温度差⊿thを計算します。
⊿th=7,671/{(4,190/0.835)×1.006×(1,000/3,600)}≒5.47[K]
ここで0.835は暖房室内条件下における空気の比容積[m3/kg]注1なのですが、煩雑なら空気の密度の概算値1.2[kg/m3]を乗じてもかまいません。
1.006は乾き空気の定圧比熱[kJ/kg・K]です。
もしくは、乾き空気の容積比熱=乾き空気の定圧比熱/比容積=1.2[kJ/(m3・K)]として固定してしまう場合もあります。
【手順9】暖房時の吹出ポイント⑧をプロットします。
⑧は⑨から水平(絶対湿度一定)に温度のみを⊿th= 5.47[K]上げた状態点です
⑧と⑨を結びます。この状態線は暖房時の室内変化プロセスを示すことになります。
【手順10】暖房時の外気ポイント⑤をプロットします。
【手順11】暖房時の外気-還気混合ポイント⑥をプロットします。
冷房時と同様に外気比を計算し、外気比=0.19[-]注2、
⑤と⑨を直線で結び、(⑥-⑨)/(⑤-⑨)=0.19となるポイントが混合ポイント⑥となります。
【手順12】加熱コイル出口ポイント⑦をプロットします。
⑧から湿球温度ラインに平行な直線(湿球温度一定の状態線)を引き、
⑥から水平に引いた直線(絶対湿度一定の状態線)との交点が加熱コイル出口ポイント⑦です。
ここで⑥→⑦は加熱プロセス、⑦→⑧は水による加湿プロセスです。
注1:厳密には、比容積は吹出ポイントから室内ポイントまでの間に変化しますが、煩雑になりすぎるため、室内条件の時の値としています。
(特に、最小給気風量から逆算した値と比較しながらポイントを決定しなければならない場合などは収束計算が必要なため)
エクセル空気線図G2では低温域、高温域をサポートしているため、容積比熱としての固定値を使用せず、条件に応じた比容積を用いて計算しています。
注2:実務現場では計算プロセスが煩雑にならないよう、外気比は風量比としています。すなわち、
外気比=外気風量/全風量(ここでは空調風量)=840/4,190≒0.20[-]。
エクセル空気線図G2ではこちらの方法を用いています。
参考文献 Ref1 公益社団法人 空気調和・衛生工学会編:空気調和・衛生工学便覧(第14版),1 基礎編(2012-10)